「このテーマで一本いける」と確信した時は、たいていキャッチーなフレーズが頭に浮かぶ。一通りググってみたが同じ言い回しは見当たらなかった。本エントリでは無理数がマヂ無理になった数である「超越数」 について、自己理解の充足を兼ねた解説を記す。
そもそも無理数とはなにか
実数の世界は有理数と無理数で構成される。有理数にはわれわれが普段から親しんでいる数の大半が含まれる。ざっくばらんに言って、2つの整数を用いて分数で表せる数はすべて有理数、表せない数が無理数となる。 たとえば、整数の1、2、3… はそれぞれ$\frac{1}{1} \frac{2}{1} \frac{3}{1}$…と分数で表せるため有理数となり、0.1、0.2、0.3… のような小数も$\frac{1}{10} \frac{2}{10} \frac{3}{10}$…と変形できることから同様に有理数である。
また、小数点以下が規則的に延々と続く循環小数も有理数に含まれる。まず、循環小数 0.333… をaと置き、10倍する。この時、10aの中身は 3.333… と小数の位が繰り上がっている。10aからaを引くと9aとなり、延々と続く小数点以下の部分が除かれる。(3.333… − 0.333…) よって9a=3。aの値は$\frac{1}{3}$。したがって循環小数aは有理数として表される。
一方、代表的な無理数に$\sqrt{2}$が挙げられる。$\sqrt{2}$は絶対に整数を用いた分数で表すことができない。 なぜか?
$$ \sqrt{2}<無理 $$
仮に$\sqrt{2}$を有理数と仮定した場合、以下のように2つの整数を用いて既約分数(これ以上割れない分数)で表せなければならない。
$$ \sqrt{2}=\frac{a}{b}<無理じゃねンだわ $$
ここで両辺をともに2乗して変形すると下記の形になる。
$$ 2=\frac{a^2}{b^2}<? $$
$$ 2b^2=a^2<アワワ $$
この時、左辺に2が掛かっていることから右辺は偶数であり、aは偶数。 続いて、偶数aを 2a’ と直し、以下の形に表す。
$$ 2b^2=(2a’)^2<アッ $$
$$ b^2=2a’^2<アッアッ $$
2a’は偶数なのでbの2乗も偶数。よってbは偶数。 しかし整数a、bがともに偶数とすると、前述の 「2つの整数を用いた既約分数」 に矛盾する。(ともに偶数であればさらに割れなければならない) 以上から、$\sqrt{2}$は有理数ではない。したがって無理数である。
$$ \sqrt{2}<やっぱ無理だったはw $$
こんな具合に、整数の分数で表せない数は必ず無理数に分類される。無理数の無理は整数の分数で表すのが無理とでも暗記しておけば覚えが早い。
ところで有理数、無理数という用語の元は英語のrational、irrationalから来ているのだが、ratioの意味を自然に捉えるなら有比数とか無比数といった翻訳が適切だったのではないかと思う。分数とは比率($\frac{1}{3}$は1:3)なので、どう考えてもこっちの方が当を得ている。などと愚痴りながらググってみたら、だいたいみんな同じことを言っていた。
実際、数学用語には稀にそういった訳語の欠陥がついてまわる。そんな時は英訳を調べるとかえって腑に落ちる場合があるので是非とも試してみてほしい。
超越数=もぅマヂ無理な無理数
無理数の基礎的な説明ができたところで、ようやく本題に入る。超越数とは、無理数の中でも特別に無理みの深い数である。 具体的には、ただの無理数は代数方程式の解として存在できるのに対して、超越数は有理数係数のいかなる方程式の解にもなりえない。
$$ x^2-2=0 $$
$$ x=\pm\sqrt{2}<そんなに無理じゃねンだわ $$
たとえば普通に無理な$\sqrt{2}$は上記の2次方程式の解になりうるが、無理みが深すぎる超越数はどこにも収まる場所がない。代表的な超越数の一つに 円周率$\pi$ が挙げられる。
$$ \pi<もぅマヂ無理。 $$
知っての通り、円周率$\pi$(3.1415…)は$\sqrt{2}$と同じ無理数の仲間だが、どんなに複雑な多項式を形成しても $f(\pi)=0$ になるような解は見つからない。最大の魅力は、そんな一見トリッキーに思える超越数が、数の世界ではむしろ圧倒的多数派――われわれが普段扱う数よりもはるかに種類が多いと目されていることだ。
こんなふうに引っかかる物言いにならざるを得ないのは、複素数の多くが超越数に含まれると推定されているにも関わらず証明が非常に困難なためだ。われわれ人類は未だほとんどの数の素性を正確に把握できていないと言える。
この概念を初めて知った時に僕はなぜかHUNTER×HUNTERを思い出したね。 新大陸編の冒頭に世界地図が出てくるシーンがあっただろう。そいつがどんどんズームアウトされていって、地図より広い湖の向こう側にむちゃくちゃデカい前人未到の大陸があるって示されるやつ。さしずめ、あの世界地図の中で安全な地域が有理数で危険地帯が一部の無理数、新大陸が超越数といったところだな。
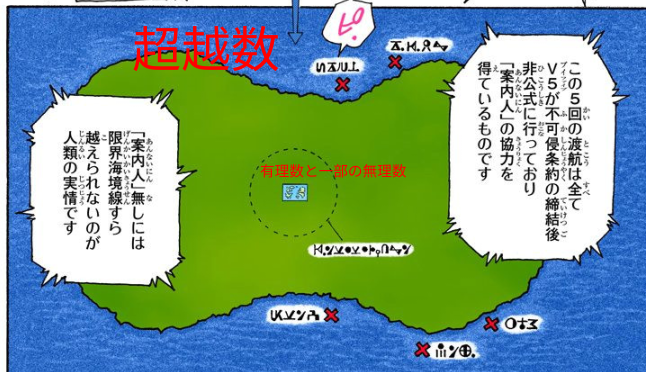
ド文系の僕でもこれには強烈なセンス・オブ・ワンダーを感じずにはいられなかった。われわれが認識している数なんて全体からすればほんのちょっとでしかないっていうのは、いかにもロマンに満ちあふれた話じゃないか。
超越数の使い道
といっても、超越数の価値はロマンだけではない。ちゃんとした使い道もある。ここでは円積問題の解決不可能性を一例にとる。当初はGeoGebraかKritaで作図するつもりだったが、面倒くさかったのでWikipediaから画像を拝借してきた。
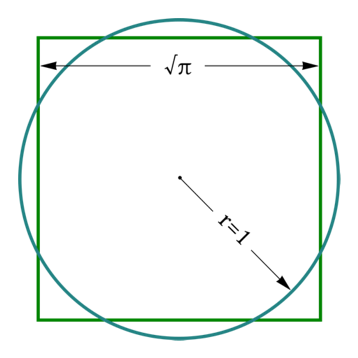
円積問題とは、ある円と等しい面積の正方形をコンパスと定規で作図できるか試すという、紀元前から19世紀の数学者たちが幾度となく挑戦しては敗れ去っていった難問である。当時は図形に学問を越えた神秘性を見出す人々がとても多かったせいか、この問題に取り憑かれる学者が後を絶たなかった。それらの試みに終止符が打たれたのが、まさしく円周率$\pi$の超越性が示された1882年。 数学者リンデマンによって行われた。

円の面積はよく知られる通り 「半径×半径×円周率$\pi$」 で表される。同様に正方形の面積は 「一辺の2乗」 で計算できる。上記の画像と同じ半径1の円の面積は1×1×$\pi$より$\pi$となるが、これと面積がまったく等しい正方形は一辺の長さが$\sqrt{\pi}$でなければならない。(2乗して$\pi$になる値は$\sqrt{\pi}$)
コンパスと定規を用いた作図は直線と円を描き、それらを手がかりに任意の交点を求め、点同士を定規で結んで線分を作成することによって行われる。一連の作業は、直線と円の交点を導く1次方程式と2次方程式の連立方程式の解に等しい。 下記に凡例を示す。
$$ 半径1の円:x^2+y^2=1 $$
$$ 直線:y=x+1 $$
直線の方程式を円の方程式に代入する。
$$ x^2+(x+1)^2=1 $$
変形し、整理すると簡素な2次方程式になる。
$$ 2x^2+2x=0 $$
これを解いて、x=0、-1。x=0の時、y=1。x=-1の時、y=0。 なお、点と直線の距離を求める公式を用いれば円の中心から直線までの距離が判り、三平方の定理で円を切り取る線分の長さも導出できる。
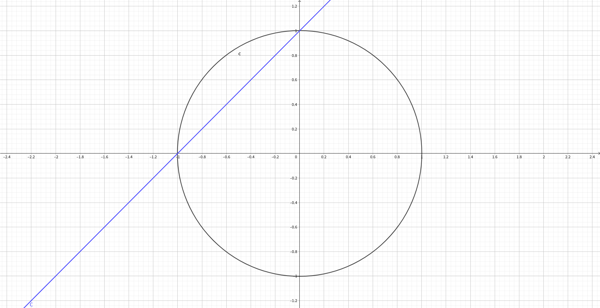
しかし前述の通り、超越数は有理数係数のいかなる方程式の解にもなりえないため、超越性を証明された円周率$\pi$ならびに$\sqrt{\pi}$の線分は作図不能である。 このようにして、超越数は古代から続く数学者たちの幻想を辛くもぶち殺したのだった。
余談だが、コンパス定規云々の話を言うなら 超越数ではない$\sqrt{2}$の線分も作図できないんじゃね? と考える人もいるかもしれない。ところが、実を言うと凡例で作図した円を切り取る線分の長さがちょうど$\sqrt{2}$になっている。
というのも、直線と円の2つの交点から円の中心までの距離がそれぞれ1なので、線分の長さが最小角45°の直角二等辺三角形の斜辺に相当するからだ。よって、三角比の法則(1:1:$\sqrt{2}$)より線分の長さは自動的に$\sqrt{2}$と定まる。これは$\sqrt{\pi}$にはまず不可能な芸当だ。
$$ \pi<無理み〜 $$
あとがき
ブログタイトルがいかにも理系じみていることもあってそろそろ数学ネタをやろうと思っていたのだが、本当に折りよく 「もぅマヂ無理数。」 とかいうしょうもない言い回しを閃いたおかげで、とりあえず一本でっち上げることができた。この閃きはまことに僥倖であったと言わざるを得ない。当面の間は僕のオリジナルとして大いに使い倒させていただく。
問題は、超越数に使い道はあってもそんな言い回しを使う局面がまるで思いつかないことである。